Canonical form of a regular vector field
Also called the "flow box coordinates theorem".

See @lee2013smooth.
It is generalized to the canonical form of commuting vector fields.
It can be expressed in term of first integrals, also:
Given the open set $U\subseteq \mathbb{R}^n$, $X \in \mathfrak{X}(U)$ and $x_0\in U$ such that $X(x_0)\neq 0$, we can find an open subset $x_0\in V\subseteq U$ such that the system
$$ \dot{x}=X(x) $$admits $n-1$ first integrals which are functionally independent and such that any other first integral depends functionally on them. (Proof [Arnold 1991]).
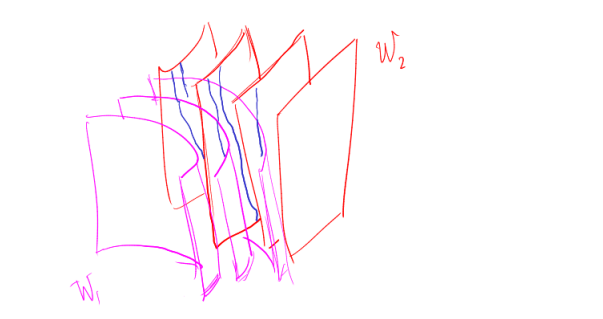
This $n-1$ first integrals $W_i$ define a curve in $V\subseteq \mathbb{R}^n$ that is precisely a solution curve $\gamma(t)$. Moreover, the $n-1$ first integrals together with the first coordinate function let us define a coordinate change
$$ \phi: (x_1, \ldots,x_n) \longmapsto (x_1,W_1, \ldots, W_{n-1}) $$so that the vector field $X$ is rectificated. Because of this this result is also called rectification lemma for vector fields.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: